梯度

梯度消失和爆炸

• deep后带来的信息传递/梯度传递问题

  • 层数过多导致？sigmoid和tanh为什么会导致梯度消失？

    1. 直观解释：从深层网络角度来讲，不同的层学习的速度差异很大，表现为网络中靠近输出的层学习的情况很好，靠近输入的层学习的很慢，有时甚至训练了很久，前几层的权值和刚开始随机初始化的值差不多。
    2. 反向传播角度解释：由于反向传播过程中，前面网络权重的偏导数的计算是逐渐从后往前累乘的，如果使用激活函数如sigmoid，导数小于一，因此累乘会逐渐变小，导致梯度消失，前面的网络层权重更新变慢；如果权重 本身比较大，累乘会导致前面网络的参数偏导数变大，产生数值上溢。
       

  • 梯度消失

    1. 原因：层数过多，学习率的大小，网络参数的初始化，激活函数的边缘效应
    2. 在深层神经网络中，每一个神经元计算得到的梯度都会传递给前一层，较浅层的神经元接收到的梯度受到之前所有层梯度的影响。如果计算得到的梯度值非常小，随着层数增多，求出的梯度更新信息将会以指数形式衰减，就会发生梯度消失。
       

  • 梯度爆炸

    1. 原因：1）隐藏层的层数过多；2）权重的初始化值过大
    2. 在深度网络或循环神经网络（Recurrent Neural Network, RNN）等网络结构中，梯度可在网络更新的过程中不断累积，变成非常大的梯度，导致网络权重值的大幅更新，使得网络不稳定；在极端情况下，权重值甚至会溢出，变为$NaN$值，再也无法更新。
    3. 解决：1）用ReLU、Leaky-ReLU、P-ReLU、R-ReLU、Maxout等替代sigmoid函数。（2）用Batch Normalization。（3）LSTM的结构设计也可以改善RNN中的梯度消失问题。（4）进行梯度裁剪(clip), 如果梯度值大于某个阈值，我们就进行梯度裁剪，限制在一个范围内.（5）使用正则化，这样会限制参数 的大小，从而防止梯度爆炸。（6）设计网络层数更少的网络进行模型训练

LSTM为什么有助于解决梯度消失和爆炸问题？

https://www.zhihu.com/question/34878706

RNN 中总的梯度是不会消失的。即便梯度越传越弱，那也只是远距离的梯度消失，由于近距离的梯度不会消失，所有梯度之和便不会消失。RNN 所谓梯度消失的真正含义是，梯度被近距离梯度主导，导致模型难以学到远距离的依赖关系。

其一是遗忘门接近 1（例如模型初始化时会把 forget bias 设置成较大的正数，让遗忘门饱和），这时候远距离梯度不消失；其二是遗忘门接近 0，但这时模型是故意阻断梯度流的，这不是 bug 而是 feature（例如情感分析任务中有一条样本 “A，但是 B”，模型读到“但是”后选择把遗忘门设置成 0，遗忘掉内容 A，这是合理的）。当然，常常也存在 f 介于 [0, 1] 之间的情况，在这种情况下只能说 LSTM 改善（而非解决）了梯度消失的状况。

激活函数

1、优秀激活函数的性质
非线性–多层后能够逼近所有函数
可导–优化器大多用梯度下降更新参数
单调–能够保证单层网络的损失函数是凸函数
近似恒等性– f(x)近似=x，参数初始化为随机小值时，神经网络更稳定
输出均值为0 – 能够加速收敛

2、激活函数输出范围
有限 – 基于梯度更新参数更稳定
无限 – 调小学习率

3、sigmoid
导数范围在0-1/4，梯度消失问题
输出均值不为0，收敛慢
幂运算耗时高

4、tanh
梯度消失
幂运算耗时高

5、 relu
缺点：
输出均值非0
dead relu – 某些神经元永远不被激活，导致相应的参数无法更新

6、dead relu改进
负数输入过多导致，改变参数初始化避免过多的负数特征送入relu，设置更小的学习率，避免参数分布巨大变化
leaky – 虽然能解决dead，但实际效果中没有证明出比relu更好

初始化建议

均值为0
标准差为 sqrt(2/当前层输入特征个数)的正太分布

指数加权平均（Exponentially weighted average）

V_t=β*V_t−1+(1−β)*θ_t

1、当 β 较大时（β = 0.98 相当于每一点前50天的平均气温)。曲线波动相对较小更加平滑，因为对很多天的气温做了平均处理，正因为如此，曲线还会右移。

较小，0.5时，曲线波动相对激烈，但是它可以更快的适应温度的变化。

2、当 β = 0.9时，我们可以近似的认为当前的数值是过去10天的平均值，但是显然如果我们直接计算过去10天的平均值，要比用指数加权平均来的更加准确。但是如果直接计算过去10天的平均值，我们要存储过去10天的数值，而加权平均只要存储V_t−1

3、指数加权平均 不能很好地拟合前几天的数据，因此需要 偏差修正
在机器学习中，多数的指数加权平均运算并不会使用偏差修正。因为大多数人更愿意在初始阶段，用一个捎带偏差的值进行运算。不过，如果在初试阶段就开始考虑偏差，指数加权移动均值仍处于预热阶段，偏差修正可以做出更好的估计。
​
V_t = V_t / (1 - β_t)

优化器

GD 到 BGD 到 SGD–即minibatch的SGD(现在说SGD一般都指MBGD)，
BGD即每次权值调整发生在批量样本输入之后，而不是每输入一个样本就更新一次模型参数。这样就会大大加快训练速度。
SGD即每次从百万数据样本中，取几百个数据点，算一个SGD梯度，更新一下模型参数。

步骤：
1、计算 t时刻损失函数关于当前参数的梯度 g_t = ▽loss
2、计算 t时刻的一阶动量m_t和二阶动量 v_t
3、计算 t时刻下降梯度 n_t = lr * m_t/sqrt(v_t)
4、计算t+1时刻的梯度即 w_t+1 = w_t - n_t

其中一阶动量是，梯度相关的函数
二阶动量是，梯度平方相关的函数

1、SGD
m_t = g_t
v_t = 1

SGD每次都会在当前位置上沿着负梯度方向更新（下降，沿着正梯度则为上升），并不考虑之前的方向梯度大小等。
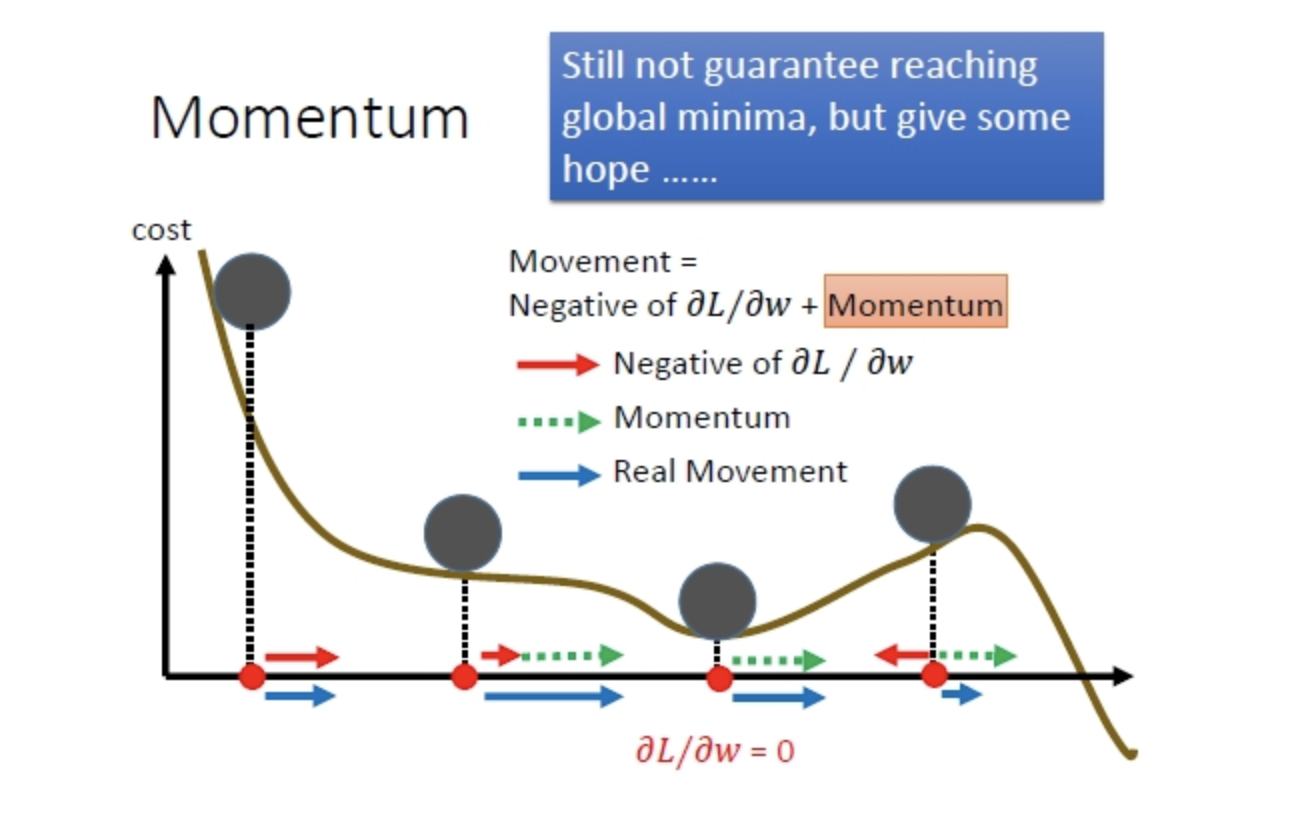
动量（moment）通过引入新的变量去积累之前的梯度（通过指数衰减平均得到），得到加速学习过程的目的。

若当前的梯度方向与累积的历史梯度方向一致，则当前的梯度会被加强，从而这一步下降的幅度更大。若当前的梯度方向与累积的梯度方向不一致，则会减弱当前下降的梯度幅度。如下图

2、SGDM 含有momentum的SGD

m_t = θ * m_t-1 + (1 - θ) * g_t – 指数加权平均
v_t = 1

初始化，m_t = 0

3、Ada 引入了二阶动量
m_t = g_t
v_t = ∑ g_t^2

优点：对于梯度较大的参数，意味着学习率会变得较小。而对于梯度较小的参数，则效果相反。这样就可以使得参数在平缓的地方下降的稍微快些，不至于徘徊不前。
缺点：由于是累积梯度的平方，到后面累积的比较大，会导致梯度消失。

在凸优化中，AdaGrad算法具有一些令人满意的理论性质。但是，在实际使用中已经发现，对于训练深度神经网络模型而言，从训练开始时累积梯度平方会导致学习率过早过量的减少。AdaGrad算法在某些深度学习模型上效果不错，但不是全部。

Adadelta
Adadelta是对Adagrad的改进，主要是为了克服Adagrad的两个缺点（摘自Adadelta论文《AdaDelta: An Adaptive Learning Rate Method》）：
the continual decay of learning rates throughout training
the need for a manually selected global learning rate

4、RMSProp
m_t = g_t
v_t = θ * v_t-1 + (1 - θ) * g_t^2

RMSprop也是对Adagrad的扩展，以在非凸的情况下效果更好。和Adadelta一样，RMSprop使用指数加权平均（指数衰减平均）只保留过去给定窗口大小的梯度，使其能够在找到凸碗状结构后快速收敛。

在实际使用过程中，RMSprop已被证明是一种有效且实用的深度神经网络优化算法。目前它是深度学习人员经常采用的优化算法之一。keras文档中关于RMSprop写到：This optimizer is usually a good choice for recurrent neural networks.

5、Adam

Adam实际上是把momentum和RMSprop结合起来的一种算法

reference:

https://ruder.io/optimizing-gradient-descent/index.html

本文作者： yuqing wang
本文链接： https://satyrswang.github.io/2021/02/04/梯度/
版权声明： 本作品采用 知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议 进行许可。转载请注明出处！

赏

thanks for tips

支付宝

微信