bagging和boosting
1、区别?
采样:随机采样(Bootstrap sampling–有放回)、加大错误样本权重
特征的采样
并行计算上
弱学习器的权重
2、从偏差和方差的角度解释bagging和boosting的原理?
bagging:
重采样、权重也相同–模型的区别性不大,bias小。
但如果假设各个子模型独立,则显著降低variance。如果完全相同的子模型,则var和单个模型一样。bagging属于两者之间,一定程度降低了var。RF特征上随机选择,进一步降低了模型的相关性,从而进一步降低了var。
boosting:
前向分步学习算法,是sequencial地减少损失函数,loss是逐步地下降的,bias也随之逐步下降。但由于是这种sequence、adaptive地,模型相关性较高,不能显著减少var。
结合策略
1平均法;2投票法:多数投票、绝对多数投票、加权投票;3学习法。
学习法,代表方法是stacking。stacking是再加上一层学习器,我们将训练集弱学习器的学习结果作为输入,将训练集的输出作为输出,重新训练一个学习器来得到最终结果。
Adaboost
1、Adaboost是模型为加法模型,学习算法为前向分步学习算法,损失函数为指数函数的分类问题。
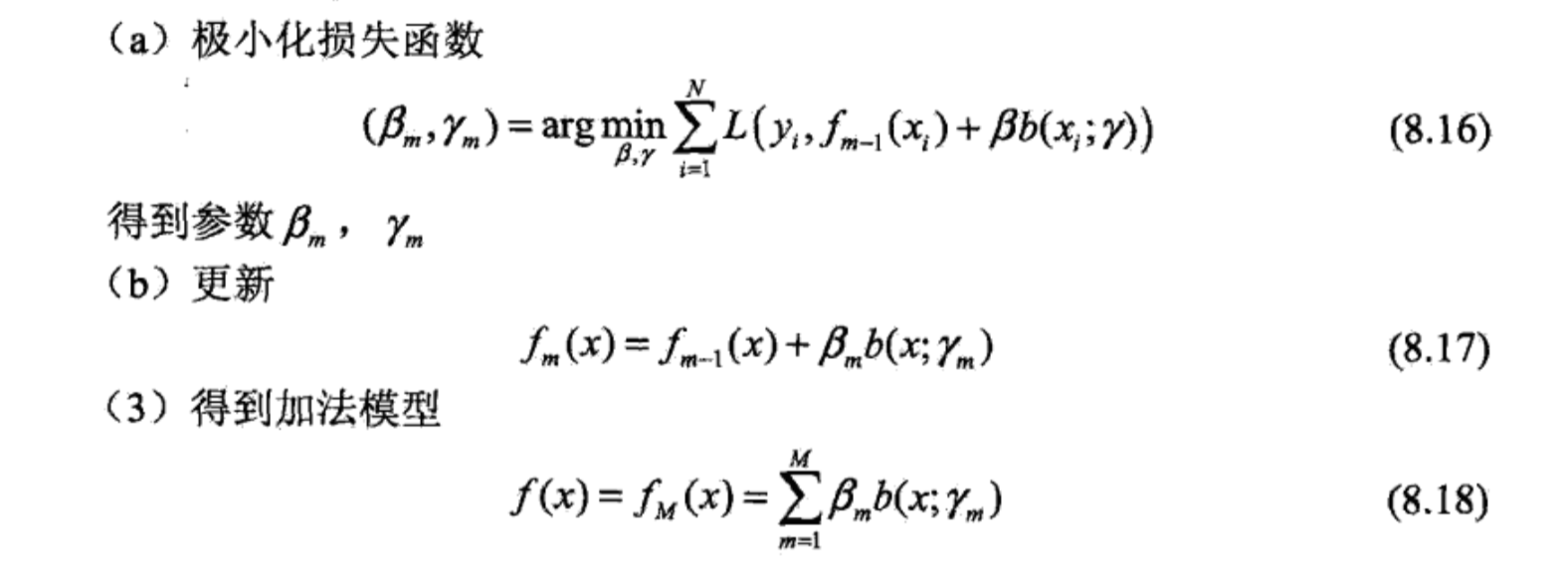
为什么loss是指数函数?证明如下:
————————————————————————————————————————————————————————————


——————————————————————————————————————————————————————————--
2、分类器结合时的权重?
由于Adaboost中若干个分类器的关系是第N个分类器更可能分对第N-1个分类器没分对的数据,而不能保证以前分对的数据也能同时分对。所以在Adaboost中,每个弱分类器都有各自最关注的点,每个弱分类器都只关注整个数据集的中一部分数据,所以它们必然是共同组合在一起才能发挥出作用。所以最终投票表决时,需要根据弱分类器的权重来进行加权投票,权重大小是根据弱分类器的分类错误率计算得出的,总的规律就是弱分类器错误率越低,其权重就越高。
计算公式:
1 误差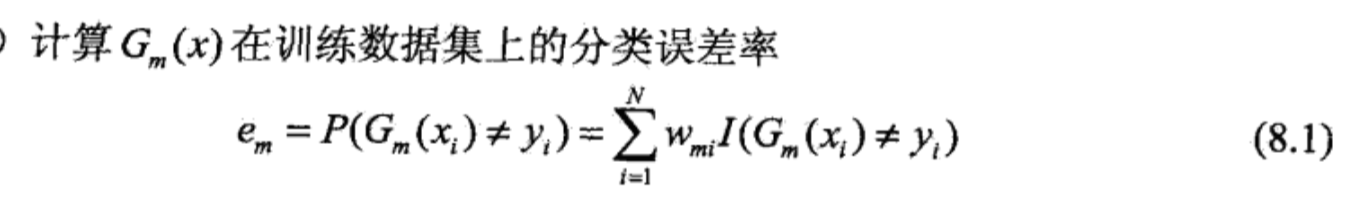
2 权重系数
3 样本权重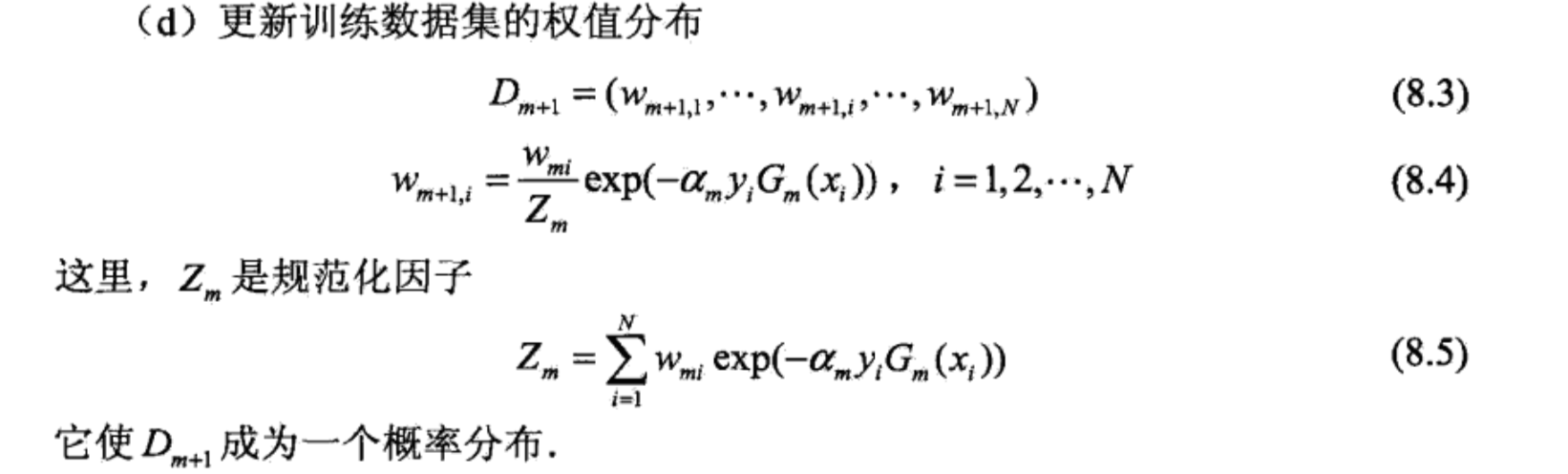
4 分类器结合及最终分类器
由上面的公式,可得到:
每次新增加一个弱分类器的时候,前面的弱分类器分错的样本的权重占总样本权重的0.5,前面弱分类器分对的样本等权重也占总样本权重的0.5。
3、正则化
fn = fn-1 + θ * a * G
θ 为正则化项
4、评价
可解释性
参数个数
performance
异常点敏感
弱分类器选择
可用于特征选择
GBDT
1、区别于adaboost
Adaboost是通过提高错分样本的权重来定位模型的不足,GBDT是通过负梯度来定位模型的不足,因此GBDT可以使用更多种类的损失函数。由于loss可以选择更鲁棒的,对于adaboost存在异常点敏感的问题,gbdt更健壮。
可以灵活处理离散和连续值。
分类的GBDT:是用指数损失函数,此时GBDT退化为Adaboost算法。
另一种方法是用类似于逻辑回归的对数似然损失函数的方法。
使用了前向分布算法,但是弱学习器限定了只能使用CART回归树模型,同时迭代思路和Adaboost也有所不同。有很多人对GBDT算法进行了开源代码的开发,比较火的是陈天奇的XGBoost和微软的LightGBM。
2、为什么只能分类树
GBDT的核心在于累加所有树的结果作为最终结果,而分类树的结果显然是没办法累加的,所以GBDT中的树都是回归树,不是分类树。
3、损失函数有哪些?
1指数损失;2对数损失;3均方差(如果我们选择平方损失函数,那么这个差值其实就是我们平常所说的残差。);4绝对损失;5Huber损失(它是均方差和绝对损失的折衷产物,对于远离中心的异常点,采用绝对损失,而中心附近的点采用均方差。这个界限一般用分位数点度量。);6分位数损失。56主要用于健壮回归,也就是减少异常点对损失函数的影响。
4、例子
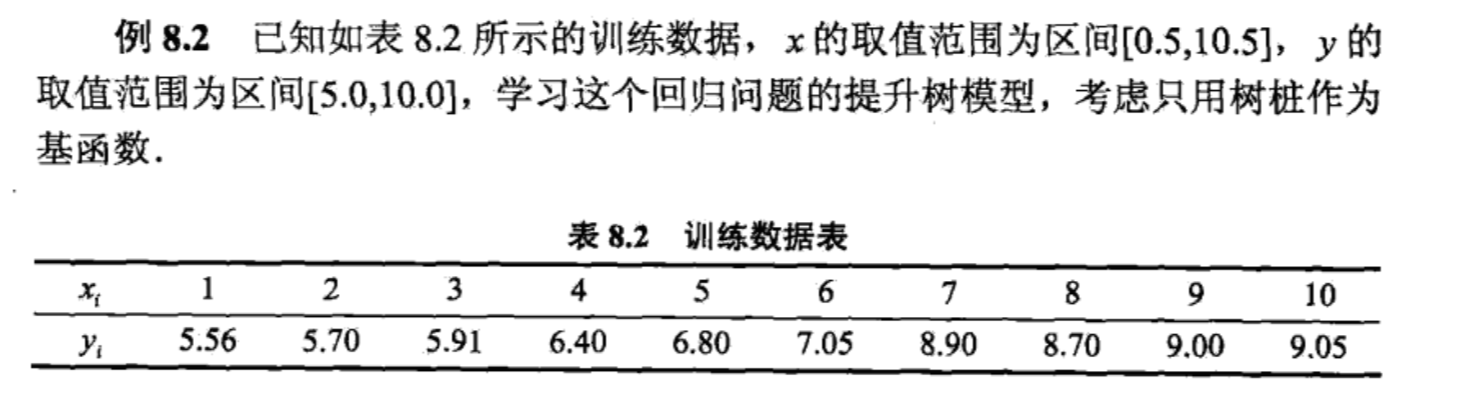
5、SGBDT
子采样比例(subsample)。取值为(0,1]。注意这里的子采样和随机森林不一样,随机森林使用的是放回抽样,而这里是不放回抽样。如果取值为1,则全部样本都使用,等于没有使用子采样。如果取值小于1,则只有一部分样本会去做GBDT的决策树拟合。选择小于1的比例可以减少方差,即防止过拟合,但是会增加样本拟合的偏差,因此取值不能太低。推荐在[0.5, 0.8]之间。使用了子采样的GBDT有时也称作随机梯度提升树(Stochastic Gradient Boosting Tree, SGBT)。由于使用了子采样,程序可以通过采样分发到不同的任务去做boosting的迭代过程,最后形成新树,从而减少弱学习器难以并行学习的弱点。
6、构造特征输入LR
如果我们想让逻辑回归处理非线性的数据,其中一种方式便是组合不同特征,增强逻辑回归对非线性分布的拟合能力。Facebook 在2014年 发表的一篇论文便是这种尝试下的产物,利用gbdt去产生有效的特征组合,以便用于逻辑回归的训练,提升模型最终的效果。如我们 使用 GBDT 生成了两棵树,两颗树一共有五个叶子节点。我们将样本 X 输入到两颗树当中去,样本X 落在了第一棵树的第二个叶子节点,第二颗树的第一个叶子节点,于是我们便可以依次构建一个五纬的特征向量,每一个纬度代表了一个叶子节点,样本落在这个叶子节点上面的话那么值为1,没有落在该叶子节点的话,那么值为 0。于是对于该样本,我们可以得到一个向量[0,1,0,1,0] 作为该样本的组合特征,和原来的特征一起输入到逻辑回归当中进行训练。实验证明这样会得到比较显著的效果提升。
7、CART分类树过程
8、相比于传统的LR,SVM效果为什么好一些
GBDT基于树模型,继承了树模型的优点 [对异常点鲁棒、不相关的特征干扰性低(LR需要加正则)、可以很好地处理缺失值、受噪音的干扰小]
处理 missing feature
数据规模影响不大,因为我们对弱分类器的要求不高,作为弱分类器的决策树的深 度一般设的比较小,即使是大数据量,也可以方便处理。像 SVM 这种数据规模大的时候训练会比较麻烦。
通常在给定的不带噪音的问题上,他能达到的最佳分类效果还是不如 SVM,逻辑回归之类的。
实际问题中,往往有很大的噪音,使得 Decision Tree 这个弱势就不那么明显了。
9、加速训练?
是否预排序,预排序可以加速查找最佳分裂点(不确定).在样本规模上的并行计算。
10、参数
第一类Miscellaneous Parameters
第二类:Boosting Parameters:
n_estimators 最大弱学习器的个数,太小欠拟合,太大过拟合
learning_rate 学习率,太大过拟合,一般很小0.1,和n_estimators一起调
subsample 子采样,防止过拟合,太小欠拟合。GBDT中是不放回采样第三类:Tree-Specific Parameters
max_features 最大特征数
max_depth 最大树深,太大过拟合
min_samples_split 内部节点再划分所需最小样本数,越大越防过拟合
min_weight_fraction_leaf 叶子节点最小的样本权重和。如果存在较多样本有缺失值,或者分类树样本的分布类别偏差很大,就会引入样本权重,这时我们就要注意这个值了。越大越防过拟合
max_leaf_nodes:最大叶子节点数 ,太大过拟合
min_impurity_split:节点划分最小不纯度
presort:是否对数据进行预分类,以加快拟合中最佳分裂点的发现。默认False。非稀疏数据则预排序,若稀疏数据则不预排序。小规模数据预排序。
11、调参思路
1、首先使用默认的参数,进行数据拟合;
2、从步长(learning rate)和迭代次数(n_estimators)入手;一般来说,开始选择一个较小的步长来网格搜索最好的迭代次数。这里,可以将步长初始值设置为0.1。对于迭代次数进行网格搜索;
3、接下来对决策树的参数进行寻优
4、首先我们对决策树最大深度max_depth和内部节点再划分所需最小样本数min_samples_split进行网格搜索。【min_samples_split暂时不能一起定下来,因为这个还和决策树其他的参数存在关联】
5、接着再对内部节点再划分所需最小样本数min_samples_split和叶子节点最少样本数min_samples_leaf一起调参;做到这里,min_samples_split要做两次网格寻优,一次是树的最大深度max_depth,一次是叶子节点最少样本数min_samples_leaf。
【具体观察min_samples_split的值是否落在边界上,如果是可以进一步寻优】
6、继续对最大特征数max_features进行网格搜索。做完这一步可以看看寻找出的最优参数组合给出的分类器的效果。
7、可以进一步考虑对子采样的比例进行网格搜索,得到subsample的寻优参数
8、回归到第2步调整设定的步长(learning rate)和迭代次数(n_estimators),注意两者的乘积保持不变,这里可以分析得到:通过减小步长可以提高泛化能力,但是步长设定过小,也会导致拟合效果反而变差,也就是说,步长不能设置的过小。
mind:
本文链接: https://satyrswang.github.io/2021/02/21/提升方法/
版权声明: 本作品采用 知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议 进行许可。转载请注明出处!


