本文主要介绍 线性链的CRF。应用于标注问题。
介绍:概率图、MEMM问题、势函数、CRF的定义和表示方法,以及基本问题。
00概率无向图模型
1、无向图表示的随机变量之间:成对马尔科夫性、局部马尔科夫性、全局马尔科夫性。
2、概率无向图模型定义:
联合概率满足上面的三个马尔科夫性,则称此联合概率分布为概率无向图模型或者马尔科夫随机出。
3、团与最大团
4、因子分解
联合分布表示为 最大团上的随机变量的函数的乘积形式的操作,称为概率无向图模型的因子分解。
这个函数,就是 势函数。要求是正的。一般为指数函数。
5、条件随机场
给定随机变量x的条件下,随机变量y的马尔科夫随机场。
学习时,学习条件概率模型。预测时利用条件概率,求得最大输出序列y。
定义:


01引入
MEMM有的缺陷是标签偏向。
标签偏向问题的原因是 – MEMM在每一步都用softmax进行了归一化
CRF通过全局归一化解决了标签偏向问题。
这样讲是比较费解的。论文里的例子容易理解。两个词,rib rob。
概率图如下(来自论文)
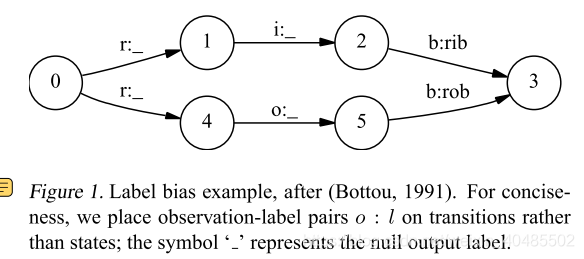
这里隐状态1到2只有一条路,4到5也只有一条路,所以整个模型没有考虑观测值i 和 o不同,所以导致词性标注过程中,不考虑观测变量。这个就不符合逻辑了。
因此局部的归一化,容易受隐变量影响,而不去考虑观测变量。这个带来的问题是:
如果training数据,3个都是rib,一个是rob。那么在预测过程中,求max P(y1y2y3|rob)时,viterbi算法走出来的,将会是0->1->2->3。
即,如果上一个状态是低熵的,那么很容易忽略观测变量,而在预测时,受样本影响较大。
即,无论观测值,当State1比State2转移少,State1会一直转移到State1,即使全局看转移到State2概率更高。即有更少转移的状态、拥有的转移概率普遍偏高,概率最大路径更容易出现转移少的状态。
02CRF解决label bias
一,crf将输入序列和输出标注映射为一个d维实数向量,而MEMM的特征函数拥有的信息只是输入序列和当前状态以及上一个状态,也就是说CRF的特征函数掌握信息量更多,从而表达能力更强。
第二个的改进是它不再每一次状态转移进行归一化,而是在全局进行归一化,这样完美解决Label Bias问题。即CRF统计了全局概率,在做归一化时考虑了数据在全局的分布,而不是仅仅在局部归一化,这样就解决了MEMM中的标记偏置的问题。使得序列标注的解码变得最优解。
有得必有失,注意到模型的分母需要罗列所有的状态序列,对于序列长度为n的输入序列,状态序列的个数为S^n ,对于这种指数增长问题,在实际应用中一般都是intractable的,只能付诸于近似求解,比如我们之前提过的Variational Bayes或者Gibbs Sampling等等。
不过有一种特殊结构的CRF – linear chain crf,精确快速求解的方式是存在的。
(注:马尔科夫随机场就是概率无向图,而crf是马尔科夫随机场特殊一种,而线性链是crf的特殊一种。隐状态是随机场,而观测变量是条件。条件随机场还有其他多种形式。)
03最大图、势函数
举个例子
例子更清楚:
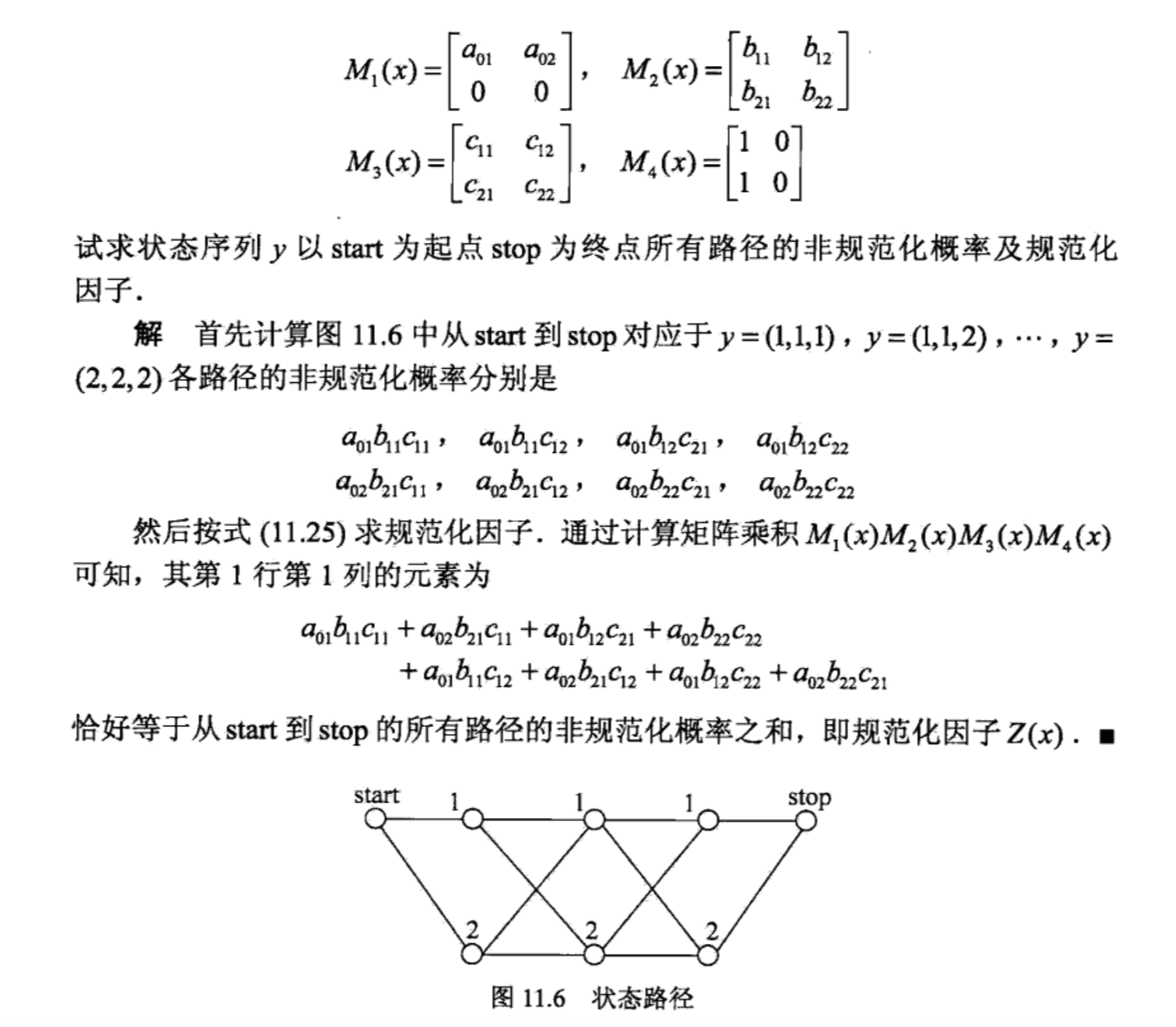
linear crf 是如何定义特征函数的?如何将原来intractable的问题变为tractable?
linear让最大团的个数为序列长度-1,并且,最大团内部的特征函数为 t1 个状态特征函数 和 t2个转移特征函数 之和的形式。
那,无向图的条件概率怎么表达呢?
从MEMM可见,本质上有两点,一是x到y的函数,即自定义的特征函数,二是loss。和MEMM不同的是,CRF是无向图。无向图的条件概率怎么表达呢?
来自google图片
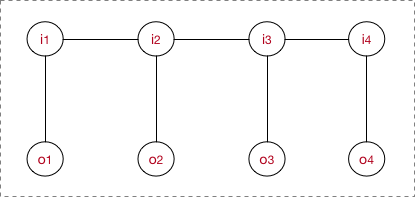
这里就引入了最大团概念。由上文介绍。得到
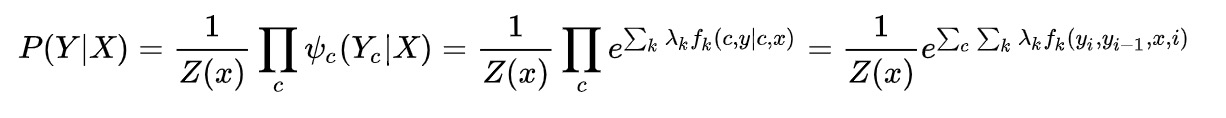
这个公式,本质是求 观测变量下隐状态序列的概率。c为最大团个数,k为自定义的k个特征函数。
对于CRF,可以为他定义两款特征函数:转移特征&状态特征。 即将建模总公式展开,见下面👇的参数化表达。
省得写了,下面大量贴图。
04三种表达形式
1、参数化形式
公式:
解释如下: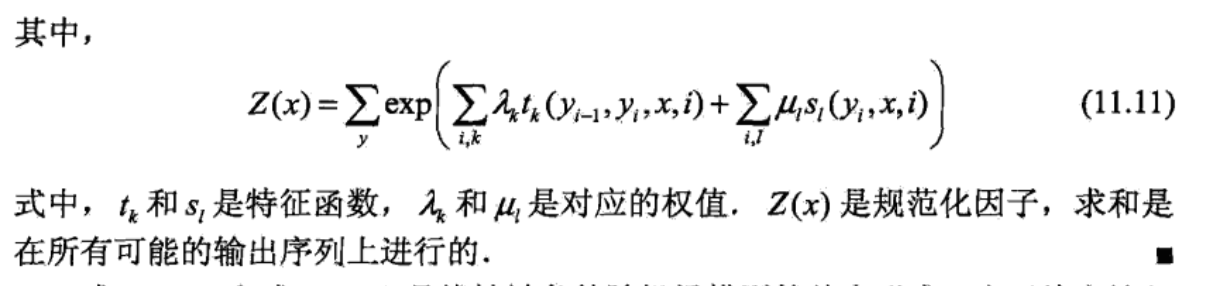

即: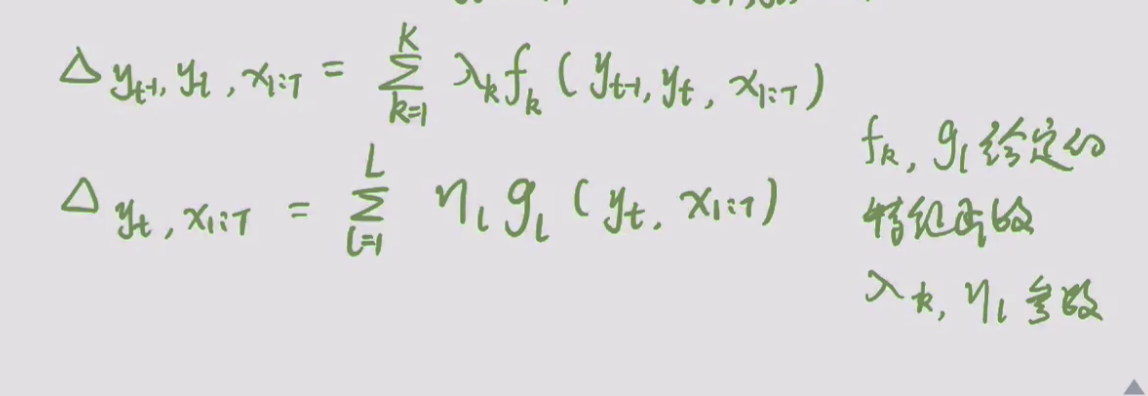
把两种特征合在一起:
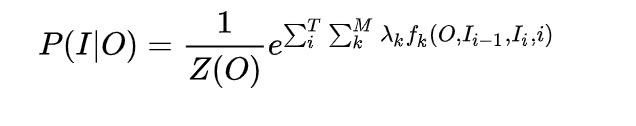
合并的公式中,我们并没有显示将边和节点区分开来,而只是写出了边的特征函数,因为从某种程度上边包含的信息已经涵盖了节点所拥有的信息,将两者统一起来可以有利于我们数学公式表达的方便性,另一方面,将边和节点进行单独讨论,从理论上可能有一点冗余,但是从实际效果中,节点信息可以充当一种backoff,起到一定的平滑效果(Smoothing)。
特征函数部分和MEMM一样记做score:
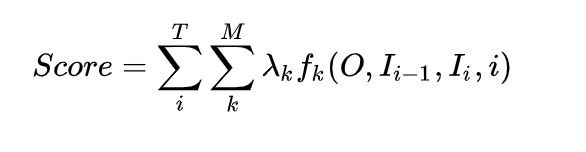
可见:
我们为 token(隐状态) 打分,满足条件的就有所贡献。最后将所得的分数进行log线性表示,求和后归一化,即可得到概率值。对数线性的思路。
这个的推导在视频里去看。https://www.bilibili.com/video/BV19t411R7QU?p=4
2、参数化简化的形式推导
略
3、矩阵形式
矩阵形式推导:
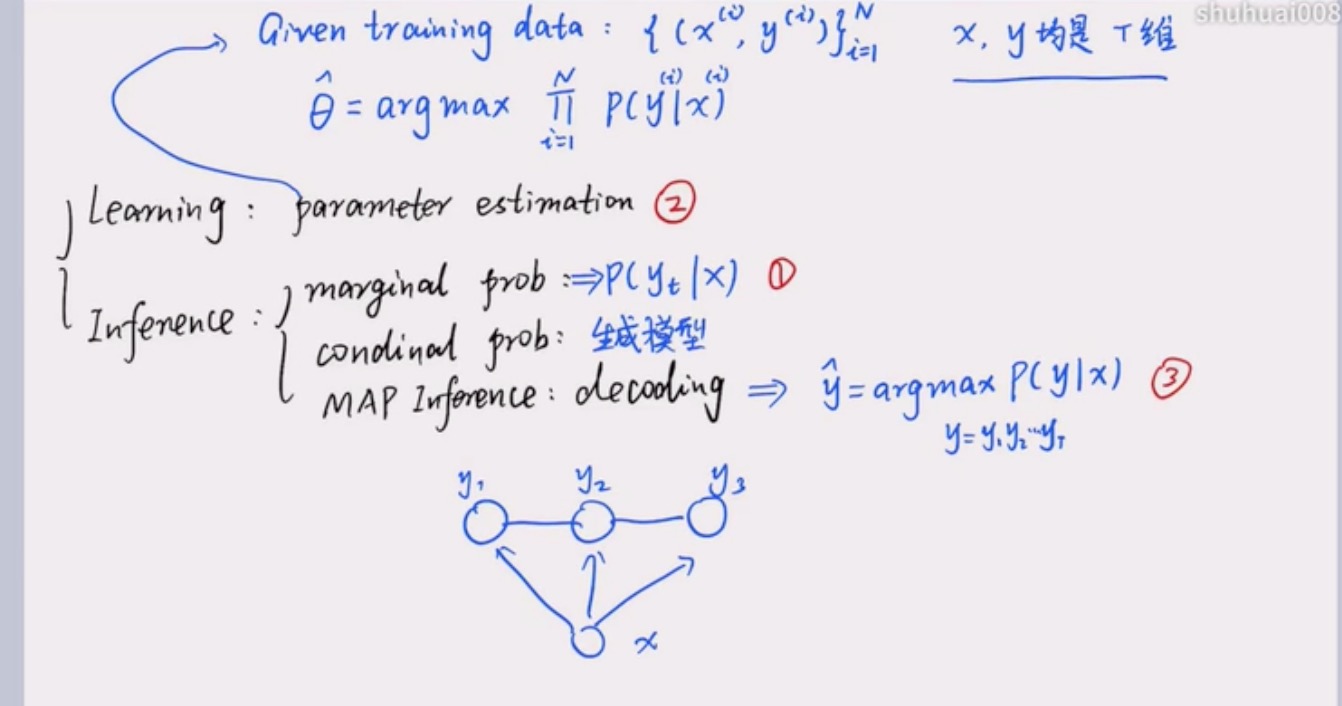
05三个问题
模型基本问题
模型问题包含 learning 和 inference。
learning即 parameter estimation。求 θ。
inference:
(以下 y 为隐变量)
1 marginal prob : 当建模对象为joint distribution,求p(y_t|x)即求边缘概率问题。
2 conditional prob : 求 p(x|y) –此为生成模型才有的问题,在crf中不考虑
3 MAP inference : decoding , 求 y_pred = argmax p(y|x) 其中y_pred = y_1y_2y_3 …
CRF learning
1、问题定义
CRF也是极大似然估计方法、梯度下降、牛顿迭代、拟牛顿下降、IIS、BFGS、L-BFGS等等。能用在log-linear models上的求参方法都可以用过来。
2、todo – 数学推导
CRF marginal prob
1、即求 P(yt = i | x)
给定x条件下的 隐变量yt 的边缘概率。
即 词性标注中,给定一句话,判断出 y1(第一个词)是动词(i)的概率是多少。
2、硬算,复杂度高。指数级计算不可行。
简化:
数学转化。
用到了变量消除法, sum+product,又叫信念传播,belief propagate。
HMM的前向 后向传播也就是belief propagate。


CRF decoding
求 y的序列,使得 argmax p(y|x)
– 类似于 HMM 问题。vertbi,既然是dp,核心要梳理清楚dp的转移函数。
我们就定义i处的局部状态为 f(I) ,表示在位置i处的隐状态的各种取值可能为 I,然后递推位置i+1处的隐状态,写出来DP转移公式。
reference
https://arxiv.org/abs/1011.4088
http://www.ai.mit.edu/courses/6.891-nlp/ASSIGNMENT1/t11.1.pdf
https://www.cnblogs.com/en-heng/p/6201893.html
https://blog.csdn.net/aws3217150/article/details/68935789
本文链接: https://satyrswang.github.io/2021/03/09/CRF/
版权声明: 本作品采用 知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议 进行许可。转载请注明出处!


