概率图
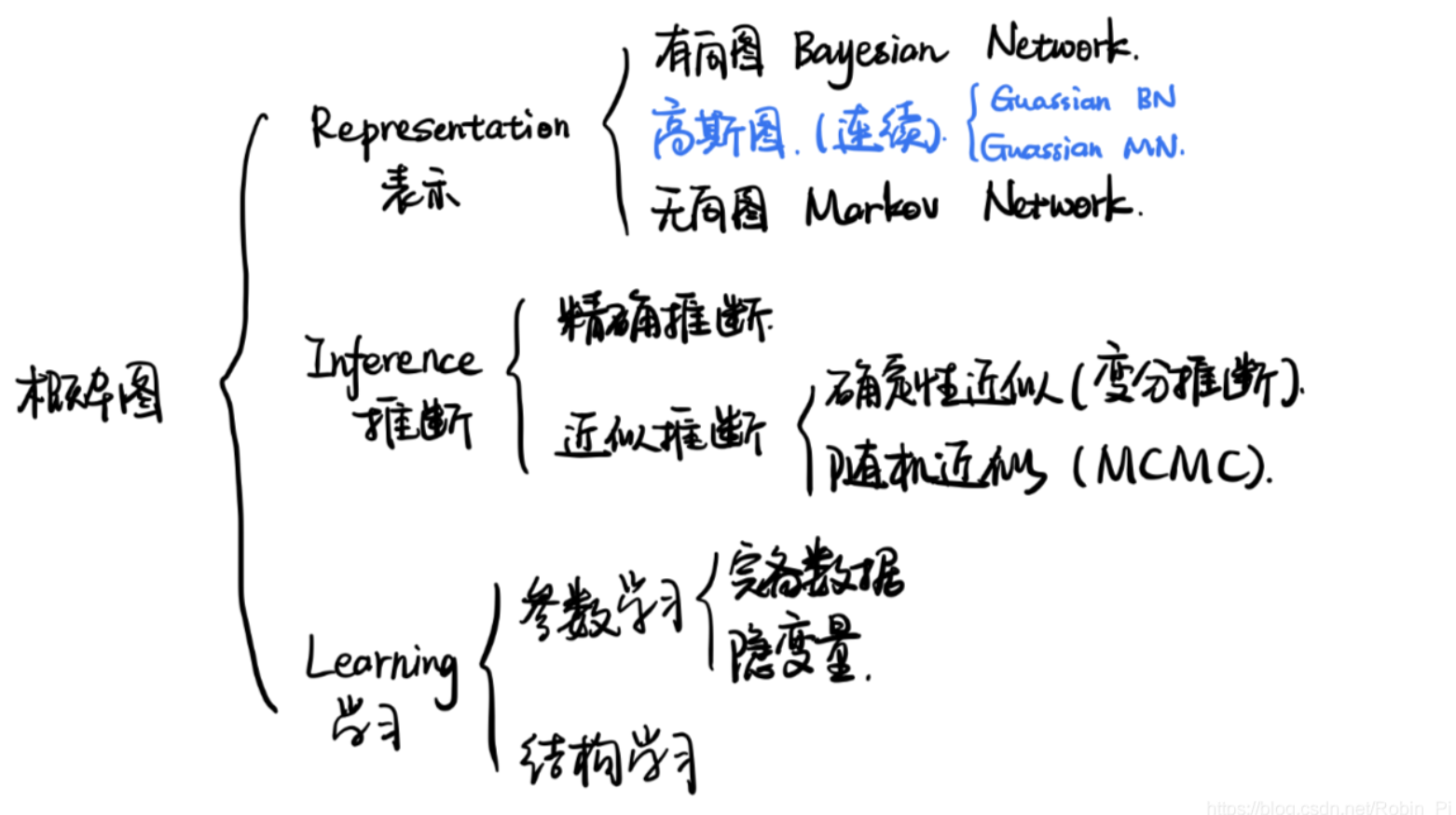
概率图模型分为贝叶斯网络(Bayesian Network)和马尔可夫网络(Markov Network)两大类。
贝叶斯网络可以用一个有向图结构表示,马尔可夫网络可以表示成一个无向图的网络结构。若随机变量Y构成一个无向图 G=(V,E)表示的马尔科夫随机场(MRF),则条件概率分布P(Y|X)称为条件随机场(Conditional Random Field, 简称CRF。
更详细地说,概率图模型包括了朴素贝叶斯模型、最大熵模型、隐马尔可夫模型、条件随机场、主题模型等,在机器学习的诸多场景中都有着广泛的应用。
频率派与贝叶斯派
频率派与贝叶斯派各自不同的思考方式:
频率派把需要推断的参数θ看做是固定的未知常数,即概率虽然是未知的,但最起码是确定的一个值,同时,样本X 是随机的,所以频率派重点研究样本空间,大部分的概率计算都是针对样本X 的分布;
而贝叶斯派的观点则截然相反,他们认为参数是随机变量,而样本X 是固定的,由于样本是固定的,所以他们重点研究的是参数的分布。
贝叶斯派既然把概率看做是一个随机变量,所以要计算概率的分布,便得事先知道的无条件分布,即在有样本之前(或观察到X之前),有着怎样的分布呢?这种在实验之前定下的属于基本前提性质的分布称为先验分布,或着无条件分布。
其中,先验信息一般来源于经验跟历史资料。而后验分布π(θ|X)一般也认为是在给定样本X的情况下的θ条件分布,而使π(θ|X)达到最大的值,称为最大后验估计,类似于经典统计学中的极大似然估计。
判别和生成
常见的概率图模型有朴素贝叶斯、最大熵模型、贝叶斯网络、隐马尔可夫模
型、条件随机场、pLSA、LDA等。
朴素贝叶斯、贝叶斯网络、pLSA、LDA等模型都是先对联合概率分布进行建模,然后再通过计算边缘分布得到对变量的预测,所以它们都属于生成式模型;而最大熵模型是直接对条件概率分布进行建模,因此属于判别式模型。隐马尔可夫模型和条件随机场模型是对序列数据进行建模的方法,将在后面的章节中详细介绍,其中隐马尔可夫模型属于生成式模型,条件随机场属于判别式模型。

我的视频讲解(https://www.bilibili.com/video/BV16y4y187pE)
解释朴素贝叶斯算法里面的先验概率、似然估计和边际似然估计?
先验概率:就是因变量(二分法)在数据集中的比例。这是在你没有任何进一步的信息的时候,是对分类能做出的最接近的猜测。
似然估计:似然估计是在其他一些变量的给定的情况下,一个观测值被分类为1的概率。例如,“FREE”这个词在以前的垃圾邮件使用的概率就是似然估计。
边际似然估计:边际似然估计就是,“FREE”这个词在任何消息中使用的概率。
贝叶斯网络
贝叶斯网络(Bayesian network),又称信念网络(Belief Network),或有向无环图模型(directed acyclic graphical model)
例子: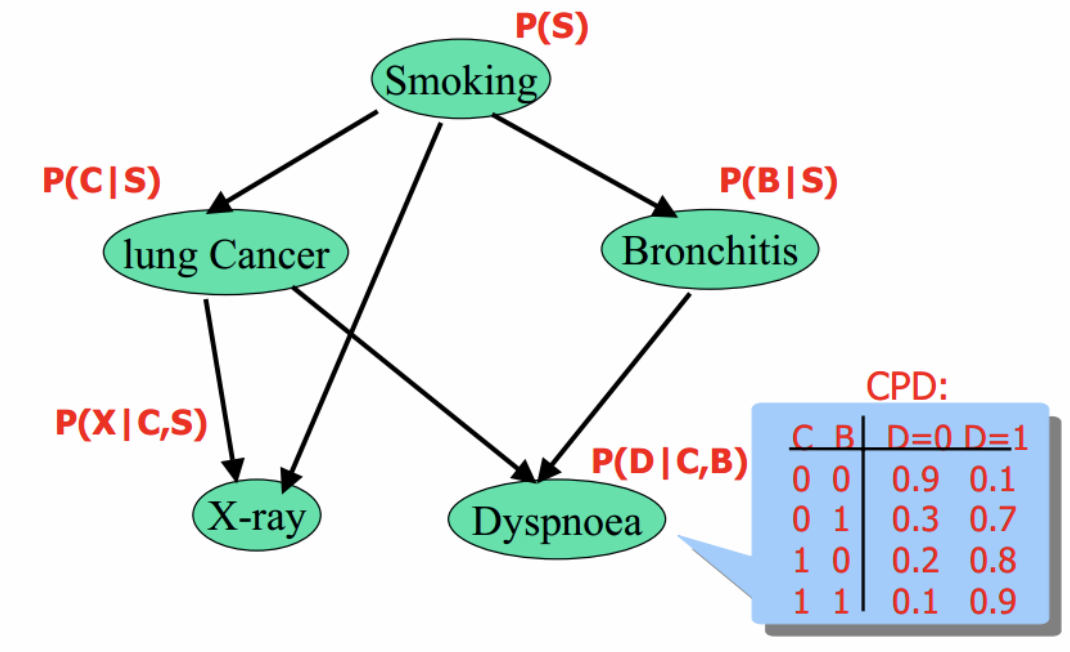
结构形式
1、 a->c b->c
P(a,b,c) = P(a)P(b)P(c|a,b)成立,即在c未知的条件下,a、b被阻断(blocked),是独立的,称之为head-to-head条件独立。
2、c->a c->b
考虑c未知,跟c已知这两种情况:
在c未知的时候,有:P(a,b,c)=P(c)P(a|c)P(b|c),此时,没法得出P(a,b) = P(a)P(b),即c未知时,a、b不独立。
在c已知的时候,有:P(a,b|c)=P(a,b,c)/P(c),然后将P(a,b,c)=P(c)P(a|c)P(b|c)带入式子中,得到:P(a,b|c)= P(a|c)*P(b|c),即c已知时,a、b独立。
3、a->c->b
还是分c未知跟c已知这两种情况:
c未知时,有:P(a,b,c)=P(a)P(c|a)P(b|c),但无法推出P(a,b) = P(a)P(b),即c未知时,a、b不独立。
c已知时,有:P(a,b|c)=P(a,b,c)/P(c),且根据P(a,c) = P(a)P(c|a) = P(c)P(a|c),可化简得到: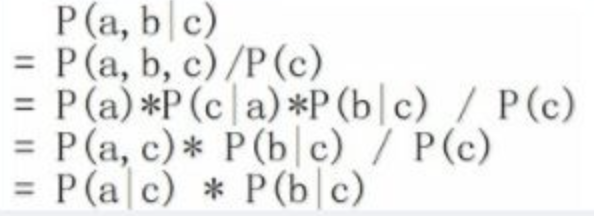
所以,在c给定的条件下,a,b被阻断(blocked),是独立的,称之为head-to-tail条件独立。
这个head-to-tail其实就是一个链式网络。
因子图
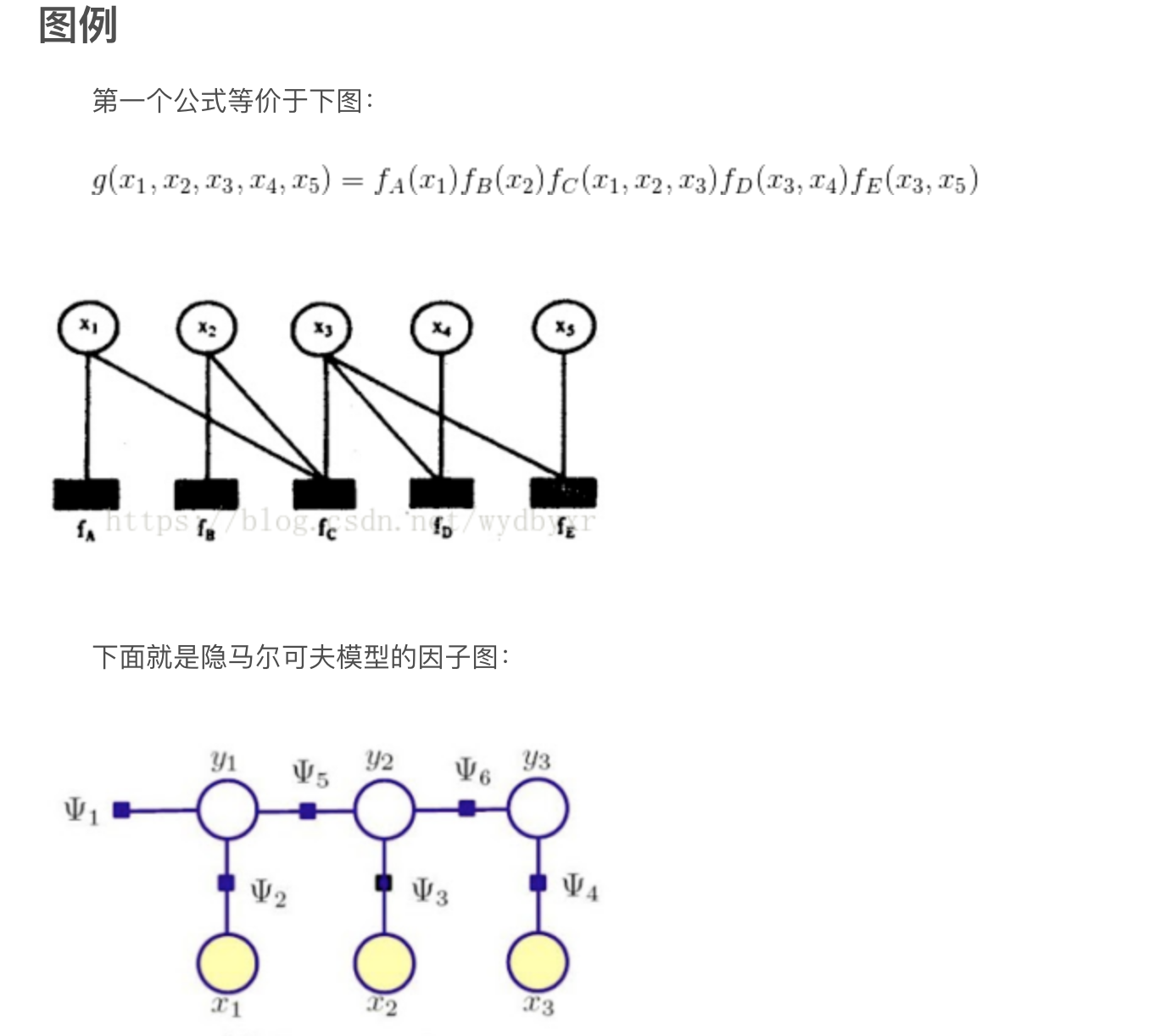
wikipedia上是这样定义因子图的:将一个具有多变量的全局函数因子分解,得到几个局部函数的乘积,以此为基础得到的一个双向图叫做因子图(Factor Graph)。
通俗来讲,所谓因子图就是对函数进行因子分解得到的一种概率图。一般内含两种节点:变量节点和函数节点。我们知道,一个全局函数通过因式分解能够分解为多个局部函数的乘积,这些局部函数和对应的变量关系就体现在因子图上。
根据贝叶斯网络的例子,

内容
1、求某个变量的边缘分布是常见的问题:这问题有很多求解方法,其中之一就是把贝叶斯网络或马尔科夫随机场 转换成 因子图,然后用sum-product算法求解。换言之,基于因子图可以用sum-product 算法高效的求各个变量的边缘分布。
2、
reference:
https://blog.csdn.net/v_july_v/article/details/40984699
本文链接: https://satyrswang.github.io/2021/03/13/贝叶斯网络/
版权声明: 本作品采用 知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议 进行许可。转载请注明出处!


