从HMM MEMM介绍概率图、生成和判别模型
简述
我理解,机器学习,本质是一种反向求解过程。数据的具象世界里找到抽象的规律。比由规律推演出具象要复杂。
并且反向求解还有各种现实的局限,数据上、算力上、可行性上、性能约束上。就会有各种trick。就像工程中缓存击穿穿透问题,通过小trick来避免。而其根基还是在于统计。
由机器学习到深度学习,根基和理论框架都没有变。
CRF即是一种对序列数据的建模。放松了HMM的1-gram依赖假设和观测独立假设。转移和发射矩阵也进一步抽象为函数。因此就比HMM更实际些。也由于放松, 需要各种理论(和SVM一样涉及到了许多定理,更多是概率统计里分布相关的定理)支持,就比HMM 更加复杂。
很容易从概率图,看到机器学习为何向深度转化。本质都是对现实世界里的学习任务进行建模。
00 生成和判别模型
概率图为什么那么难。核心在 是否理解 生成和判别模型的区别。
神经网络模型、SVM、perceptron、LR、DT……
NB、LDA ……
核心区别在于: 对 联合概率 还是对 条件概率 建模。
角度一用inference过程举例:假设我知道P(X) P(X,Y) ,那我就根据条件概率公式预测出来y_pred 了。
这个是 生成模型。
而判别 : 假设我知道P(Y|X) ,那我直接代入X就可得到y_pred
角度二用learning过程举例:生成我要对 P(X,Y) 建模,判别我要对P(Y|X) 建模。
其实是很简单的。但是我们 对于不同模型去整体把握的时候 ,忽略了top down思维方式。bottom up的确是不容易想清楚。
进一步: 你能从这里思考出,生成和判别的各自局限吗?
判别边界和(结果的)生成过程、先验假设、数据量和性能
01 概率图
序列数据 – 标注 分类 走势分析 –>其中概率图解决标注和分类
概率图的话,需要去学习基本的有向图表示含义,图画出来(如下)则能判断,给出隐状态c,a\b之间是否独立。
来自知乎某文:
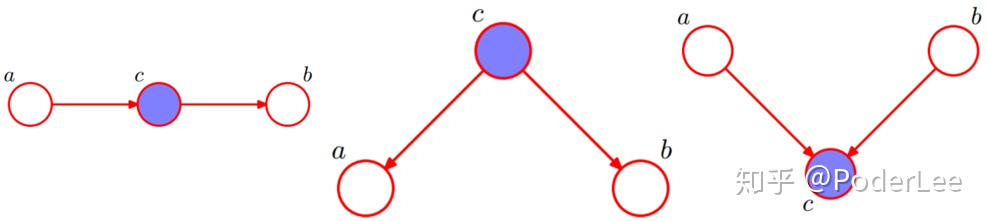
focus在HMM MEMM CRF –>如何解决标注问题
02 马尔科夫随机场定义(概率无向图定义)
马尔科夫假设 – 马尔科夫模型的前提与局限
马尔科夫性质 – a. 成对,b. 局部,c. 全局。
这个性质主要有助于无向图里势函数的推导。不在乎数学,可忽略。势函数见下04。
03 有向图和无向图
图模型 – 有向(贝叶斯网络)和无向(马尔科夫网络)
HMM、 Karman filter是有向,boltzman 、CRF是无向
核心区别:在于建模过程如何求 node 代表的token ,该随机变量的联合概率
04 无向图的联合概率 – 势函数
势函数哪里来的or为啥这个样子? – 或者说为啥无向图的联合概率是这个样子的因子分解?
: 由 Hammersley-Clifford定理 保证。
05 HMM
HMM之前的NB
来自google图片:
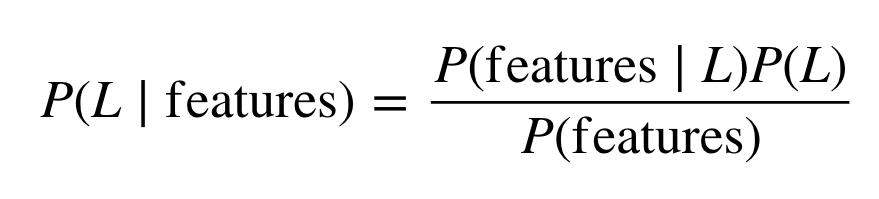
HMM五要素
第一个隐状态的概率分布、转移矩阵、发射矩阵、状态集、观测集
来自google图片:
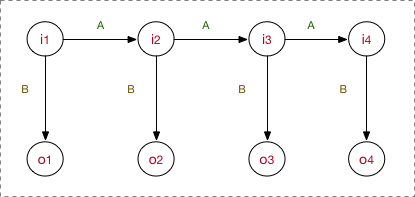
进一步: 你能从这里思考出,HMM是生成还是判别?
这也是HMM痛点。假设不合实际、生成自身局限、没有更多特征信息。
HMM问题
1、学习过程 ,即计算出五要素(建模过程)
监督学习:
MLE – 本质就是频率来估计概率
非监督学习:
Baum-Welch– 本质即EM
2、概率计算过程 ,即建好的模型下(五要素已知下),当前观测序列的联合概率
直接计算 – 本质就是个暴力穷举
前向算法、后向算法 – 本质和viterbi一样也是DP优化
3、预测过程 ,即预测出当前时刻,哪个隐状态概率最大
近似算法 – 复杂度高且是局部最优:即使当转移概率为0时,仍可能出现在预测出来的状态序列里
viterbi算法 – 本质就是个动态规划
4、filter问题
略
5、smoothing问题
略
这些算法并不需要太复杂的证明,都比较直观。这也是HMM好理解的原因。
感兴趣来bili 一键三连。
06 MEMM最大熵马尔科夫模型
整个模型的框架和HMM一样,不同之处在于:
1、观测独立的假设被打破
2、局部采用LR(最大熵模型)
3、因为2,建模过程就通过梯度下降
MEMM的概率图
来自google图片:
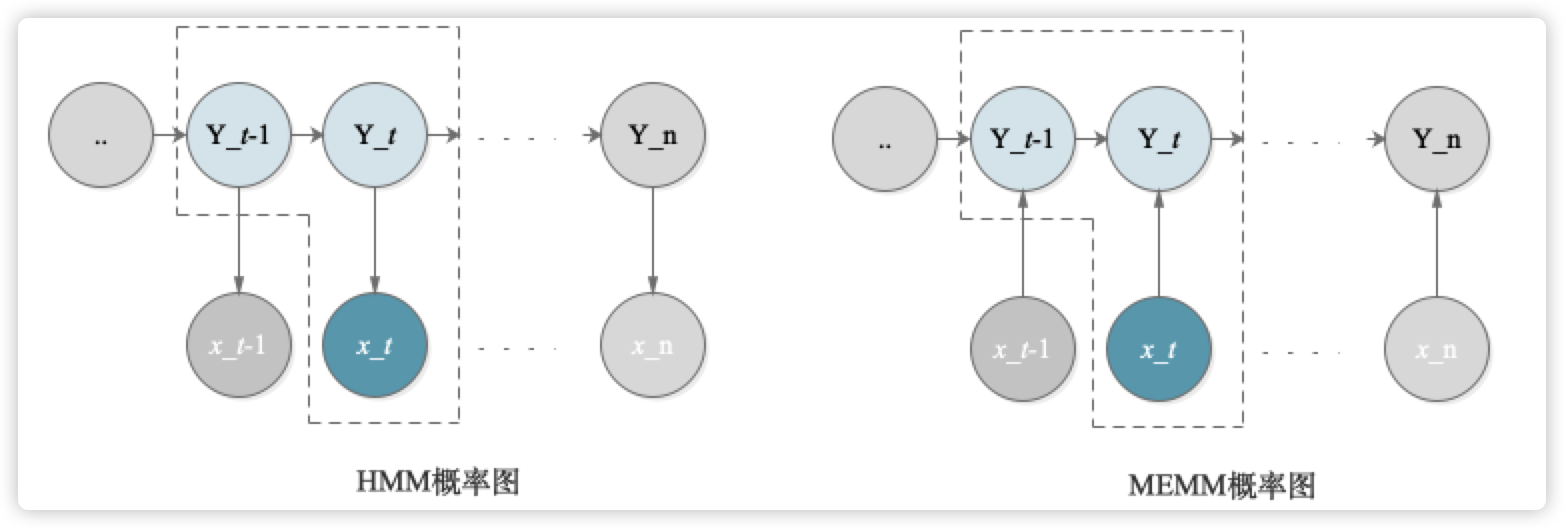
从图中可见:
1、根据01概率图的基础知识,MEMM中,当y_t已知,这种是个v字形的有向图,则x_t和y_t-1 、x_t-1 是相关的–即路径是连通的。因此打破了HMM的观测独立假设。
2、这里是判别模型,因此对P(Y|X,θ)建模
3、“x_t->y_t” 每个这个箭头的过程,都是一个逻辑回归LR。因此,每一个这样的局部都需要进行一次softmax,而softmax中e的指数是:w*f( h, y_t) ,也叫做质量分数(mass score)(这个mass来自pmf的m),其中h是 (y_t-1, x_1:t)
4、概率计算:
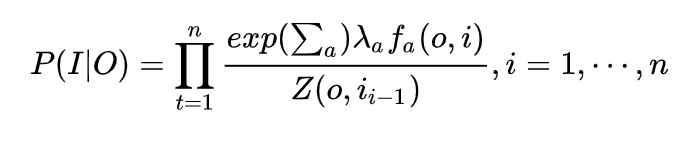
这里,就是softmax得到的隐状态y的概率,加上log就是最大似然
其中,t为第几个隐状态,i为隐状态值,o为观测值,a为不同特征函数个数–自定义,Z为softmax的归一化。
特征函数是自己定义的,可求导即可。(本质即为,从某个词到某个词性的函数)。特征函数权重是可训练参数。
相当于dfm的子网、graphsage或者GCN的聚合子网。
又找到了一个图,这个更清楚:👈🏻左边为HMM 右边👉🏻为MEMM
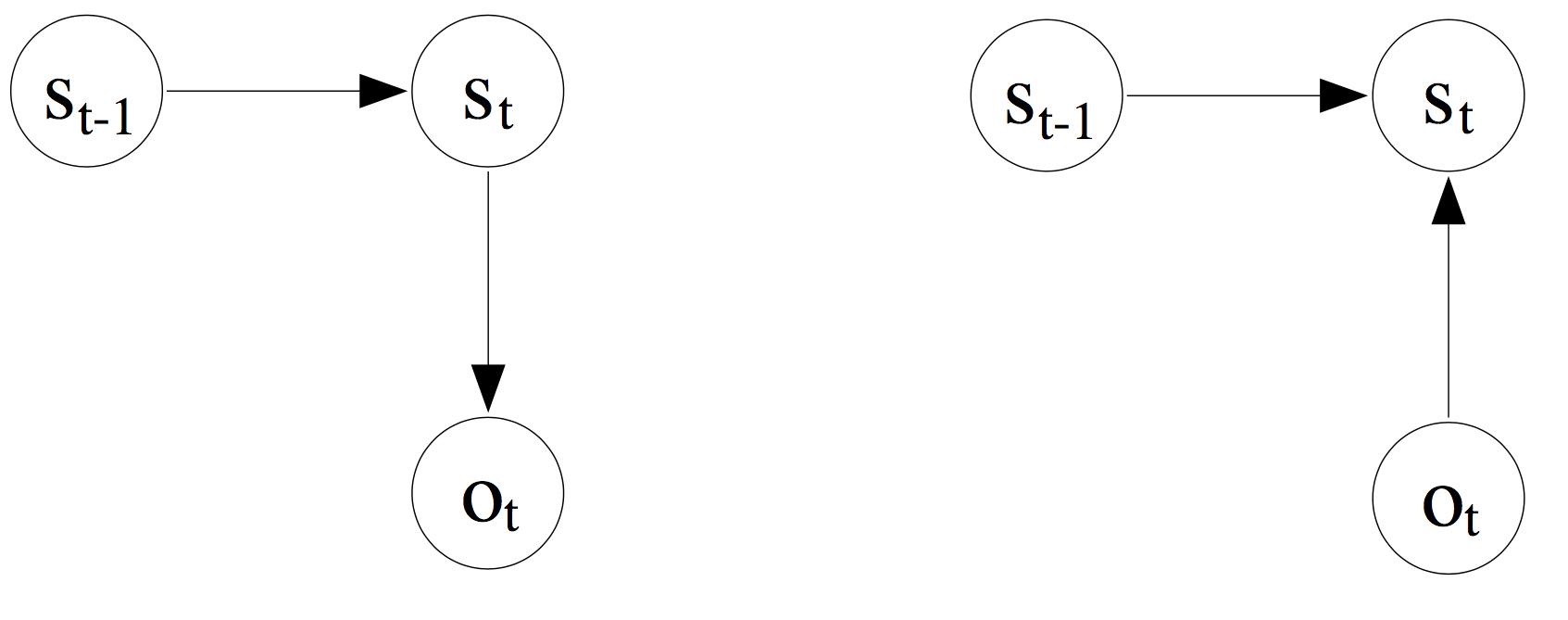
MEMM问题
和HMM一样,涉及到建模、预测。
区别的地方是:
建模:MEMM的loss是-log极大似然,然后梯度下降去求。
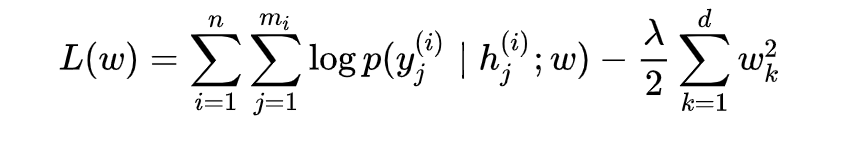
这里,对n个样本,每个样本长度为mi,的softmax结果求log,然后加了正则。
最大熵推导出softmax。整个loss的本质框架是MLE。
END
补充:
来自google图片:
NB在sequence建模下拓展到了HMM;LR在sequence建模下拓展到了CRF。
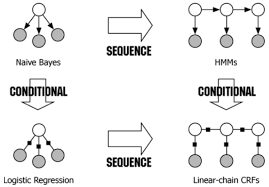
reference:
http://www.cs.columbia.edu/~mcollins/fall2014-loglineartaggers.pdf
http://www.ai.mit.edu/courses/6.891-nlp/READINGS/maxent.pdf
https://blog.csdn.net/taoqick/article/details/102672110
https://zhuanlan.zhihu.com/p/37163081
https://zhuanlan.zhihu.com/p/33397147
https://www.quora.com/What-is-the-best-resource-to-understand-Conditional-Random-Fields
谷歌图片
https://zhuanlan.zhihu.com/p/113187662
https://www.bilibili.com/video/BV19t411R7QU?p=3
本文链接: https://satyrswang.github.io/2021/04/14/CRF前续知识/
版权声明: 本作品采用 知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议 进行许可。转载请注明出处!


